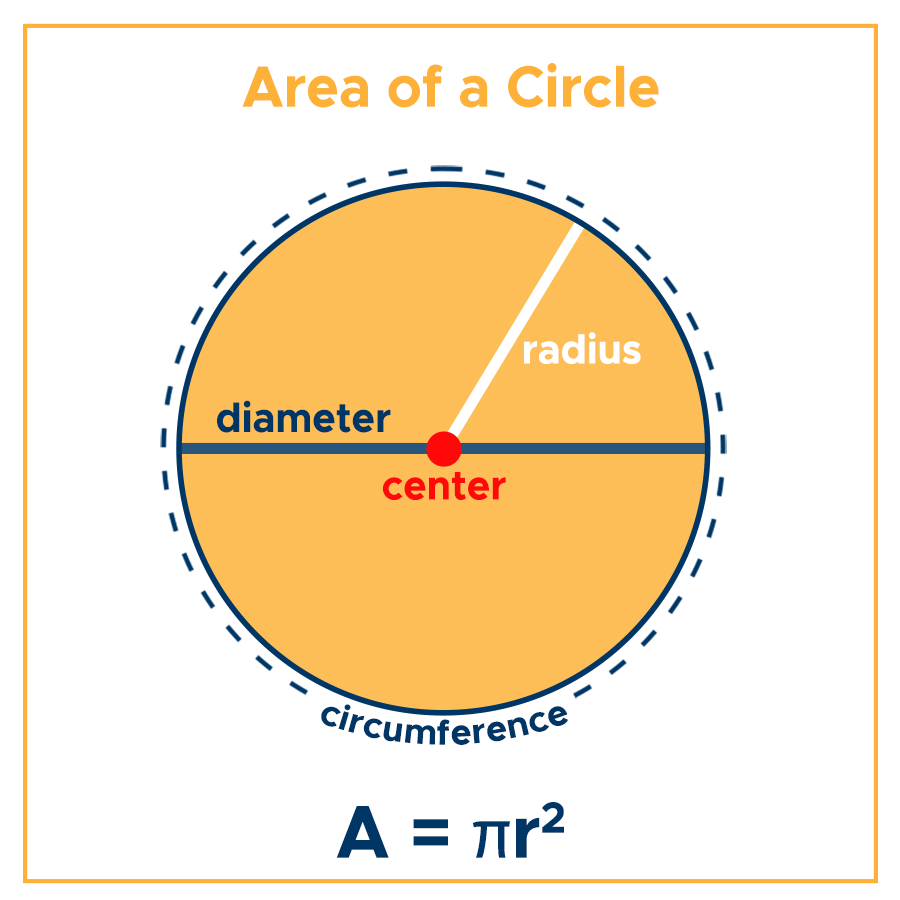
The area of a circle is the space enclosed within a circle of radius r. The area enclosed by a circle of radius r is r2. The diameter to circumference ratio is always 3.14159. The area of a circle has two properties. First, it is the same size as the diameter, which means it has the same area as the radius. Second, it is symmetrical, meaning that the circumference always lies within the radius.
Circumference
The area enclosed by a circle with radius r is the circumference times the diameter. The area contained by a circle has radius r2 and is a constant ratio of circumference to diameter (r2 = 3.14159).
In the case of circles, the area of a circle is the sum of its circumradius and base. The area of a regular polygon is 1/2ap. The length of the apothem increases with the number of sides, and eventually approaches the radius of a circle. This property allows us to determine the area enclosed by a circle. In fact, we can estimate the area of a circle by using the polygons which are inscribed in a circle.
Another method of finding the area of a circle is to divide it into 16 equal sectors. The area of each sector would be the same as the area of a parallelogram or rectangle. However, this method is not accurate. The area of a circle can vary up to four times when the diameter is doubled. In this case, the area of a circle is the sum of two areas: the radius of the circle, the diameter, and the arc length of each sector.
When calculating the area of a circle, remember that there is no volume of space inside a circle. Its area is therefore all the space enclosed by its circumference and boundary. To find the area, you need to know the radius and the base circumference of the circle. The radius of a circle is the line segment from the center to any point on the boundary of the circle. If the radius and base circumference of the circle are equal, the area of the circle is the same as the sum of those two areas.
Radius
In geometry, the radius of a circle or sphere is the length of a line segment from its center to its perimeter. It comes from the latin word radius, which means ray, but is also used to describe the spokes of a chariot wheel. So, what is the radius? How do you find out? Continue reading to find out! But first, let’s define what the radius of a circle or sphere is.
A circle’s radius is a line segment whose end lies at the center of a circle and the other lies on the edge of the circle. It is referred to as a ‘radius’ because it is constant no matter where you place it on the circle. You can find the radius of a circle using a simple circle calculator. Enter a single value and the calculator will return the area, diameter, and circumference of the circle.
If the center of the circle is at point h, then the radius of a circle is r. The center is centered at point h. Likewise, the radii are at points k and h. For instance, the radius of a circle is r = 3x + y – b. Then, if you want to know the radius of a circle, the formula for finding it is h – k + r.
To find the radius of a circle, first calculate the area of a circle in square units. For example, if a circle is 9 inches wide and 14 inches tall, the area of the circle is r/9. This is the simplest formula for finding the radius of a circle. Once you know the radius, multiply it by 3.14 to find the area. Once you have the area, you’ll know how to find the circumference of a circle.
Ununununun+un give a geometric mean
The area of a circle has a tangent to a line. The length of the tangent is the area of a circle, and its area is given by the geometric mean of the two segments a and b. We can calculate the length of a line segment by finding the area of a circle by a perpendicular to a circle.
Area
The area enclosed by a circle of radius r is equal to r2. The Greek letter r stands for the constant ratio of diameter to circumference. This ratio is 3.14159. This formula is often used to calculate the volume of a circle. Let’s look at some examples. In one example, the area of a circle is equal to 0.5 square kilometers. This formula can be used to calculate the volume of a circle or any other shape.
The area of a circle is calculated using two different methods. The first method involves using the circumference of the circle to compute the area. The second method uses pi to determine the radius. The formula is very simple. If you know the diameter of a circle, you can find its area by multiplying its circumference by its radius. If you’re not sure which one to use, try plugging in the radius first. This way, you’ll know how much area you need.
The formula for calculating the area of a circle uses the constant term p. This is also known as Archimedes’ constant. Pi is the ratio of circumference to diameter. When written as a decimal number, it equals 3.14. It is also taken as a fraction. Therefore, the area of a circle is always the same as the diameter plus its circumference. It’s important to remember that the number pi is not a prime number, but it’s still a number.
Another way to calculate the area of a circle is to measure its diameter. Most math problems will have the diameter listed as a variable. The diameter is the length of a straight line passing through the center and the edge of the circle. For small circles, use a ruler. For larger circles, use a tape measure. Next, multiply the diameter by pi. Then you’re ready to go! You’ll have a better idea of how much cloth you’ll need for a tablecloth.
Formula
The area enclosed by a circle of radius r is equal to r2. The ratio of circumference to diameter is always three, hence the Greek letter “r” which stands for constant. This ratio is 3.14159. The area of a circle is the total area of the sphere if the circle has no limbs or no center of gravity. This equation is often used to calculate the surface area of a sphere.
To calculate the surface area of a circle, we need to first compute the radius of the circle. A circle has a diameter of seven meters. Therefore, the area of a circle of seven meters is three times its radius. This means that it has an area of seven square units. If we divide the circle into three smaller rings, the result is a right triangle with a base circumference of two and an elongated base circumference of two.
The area of a circle with a radius of three meters is 80% of a similar-width square. If we consider that a circle with a radius of three meters has a diameter of three meters, the surface area of a circle of the same diameter will be approximately one and a half square meters. If we consider the radius of a pizza slice as its radius, the surface area will be 0.126 cubic meters.
Archimedes’ method of exhaustion was one of the earliest applications of mathematical limits. This axiom is a standard part of the standard analytical treatment of the real number system. However, Archimedes’ proof was not rigorous by modern standards and requires comparing two lengths. This proves the basic principle behind Fubini’s theorem. If you don’t have a good idea of how to calculate the area of a circle, then you can use the formula below.